Livro: Varian, Hal - Microeconomia (2015) - Parte XVI

                    

Livro: Varian, Hal - Microeconomia (2015) - Parte XVI

Pgs. 571-591:

CAPÍTULO 21: "Minimização de custos"

497 - "c(w1, w2, y) = Essa função é conhecida como função custo e nos será de considerável interesse". (...) À medida que deixamos o número C variar, obtemos uma família de retas isocusto. (...) Assim, o nosso problema de minimização de custos pode ser reescrito como: encontre o ponto na isoquanta que esteja associado à reta isocusto mais baixa possível. Esse ponto é ilustrado na Figura 21.1:

498 - Se tiver esquecido o que é "isoquanta": Uma isoquanta é o conjunto de todas as combinações possíveis dos insumos 1 e 2 que são exatamente suficientes para produzir determinada quantidade do produto.;

499 - Minimizar é fundir isoquanta da produção escolhida com a isocusto mais baixa. (...) a inclinação da isoquanta será igual à inclinação da curva isocusto. Ou, para usarmos a terminologia do Capítulo 19, a taxa técnica de substituição tem de ser igual à razão de preço dos fatores

500 - ...Mete uma sequência de álgebra sobre isso que nada entendi em que acrescenta. Não vou "ler".

501 - Paralelo: No problema do consumidor, a linha reta era a restrição orçamentária, ao longo da qual o consumidor se movia para encontrar sua posição preferida. No problema do produtor, a isoquanta é a restrição tecnológica e o produtor move-se ao longo dela para encontrar a posição ótima

502 - Mais conceitos antes dos problemas, claro...: As escolhas de insumos que geram custos mínimos para a empresa dependerão, em geral, dos preços dos insumos e do nível de produção que a empresa deseja ter, de modo que escrevemos essas escolhas como x1 (w1 , w2 , y) e x2 (w1 , w2 , y). Essas expressões são chamadas de funções demanda de fatores condicionadas ou demandas de fatores derivadas.

503 - Não é igual a "função de demanda de fatores", vista em capítulo anterior: A função demanda de fatores condicionada proporciona escolhas que minimizam os custos para determinado nível de produção, enquanto a função demanda de fatores que maximizam o lucro fornecem as escolhas que maximizam o lucro para determinado preço do produto. A primeira não pode ser observada, mas... é útil como forma de separar o problema da determinação do nível ótimo de produção do problema de determinar o método de produção mais efetivo em termos de custos. (Na minha cabeça, é como se ela viesse como passo seguinte, talvez seja isso, numa abordagem prática, pela qual Varian dificilmente se interessa).

504 - Axioma Fraco da Minimização de Custo (AFMC): Meu resumo ao ler as duas páginas sobre é: um monte de sopa de letras/incógnitas/álgebra para concluir coisas que uma criança de seis anos que vende limonada saberia, em pouco tempo, intuitivamente talvez. Grande exemplo de tentativa de complicar algo simples.

505 - Rendimentos constantes de escala e minimização dos custos: ...o custo mínimo para produzir y unidades de produto será de c(w1 , w2 , 1)y. No caso de rendimentos constantes de escala, a função custo é linear no produto.

506 - ...E se tivermos rendimentos crescentes de escala? Nesse caso, o custo aumenta menos do que linearmente no produto. 

507 - Mais conceito: A função de custo médio é apenas o custo unitário de produzir "y" unidades de um produto:

508 - ...Com rendimentos constantes de escala, obviamente fica:

509 - Há "função custo de curto prazo" e a "...de longo prazo". Na segunda, todos os fatores podem variar. Não há "x fixo". Em linguagem chata, assim é a de curto prazo:

510 - Quando tem só um "x1" variável e "x2" fixo a coisa é até fácil. Mas vários insumos com seus vários preços e utilidades... Enfim, se houver, porém, muitos fatores de produção variáveis no curto prazo, o problema da minimização de custos exigirá um cálculo mais elaborado.

511 - No mais, mete mais álgebras desnecessárias para ilustrar coisas óbvias. Exemplo: "...Essas equações apenas dizem, por exemplo, que, se o tamanho do prédio for fixo no curto prazo, o número de trabalhadores que a empresa deseja empregar a qualquer conjunto dado de preços ou de escolha de produção dependerá do tamanho do prédio." Ou...: "a quantidade minimizadora de custos do fator variável no longo prazo é aquela que a empresa escolheria no curto prazo – caso tivesse a quantidade de fator fixo que minimiza os custos no longo prazo".

512 - Lembra os "fatores quase-fixos". Os custos quase-fixos dão no mesmo: "só precisam ser pagos se a empresa produzir uma quantidade positiva de bens".

513 - Há custos recuperáveis e irrecuperáveis: Um gasto de US$100.000 com a compra de cinco caminhões leves parece ser bastante dinheiro, mas, se eles puderem ser vendidos mais tarde por US$80.000 no mercado de caminhões usados, o verdadeiro custo irrecuperável será de apenas US$20.000. Já um gasto de US$100.000 em uma prensa feita sob medida para estampar quinquilharias e que não tenha nenhum valor de revenda é um caso bem diferente. Tudo isso precisa ser levado em conta.

EXERCÍCIOS E APÊNDICE

514 - Mais um mix de perguntas e resposta mal formulado ou desinteressante. Coisas simples até.

515 - O apêndice mais uma vez não conseguiu atrair mais que alguns segundos do meu interesse. Não percebi qualquer dilema prático nele.

FIM DO CAPÍTULO.

Pgs. 592-614:

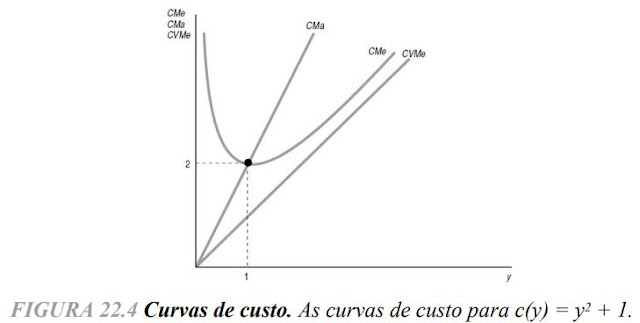
CAPÍTULO 22: "Curvas de custos"

516 - Premissas? w1 e w2 estarão congelados. "No restante deste capítulo, consideraremos constantes os preços dos fatores, de maneira que possamos escrever o custo como função apenas de y, c(y)".

517 - O total de custos da empresa pode sempre ser escrito como a soma dos custos variáveis, cv (y), e dos custos fixos, F.

518 - A função custo médio variável mede o custo variável por unidade de produção e a função custo médio fixo mede os custos fixos por unidade de produção.

519 - ... CVMe(y) representa os custos variáveis médios e CFMe(y) representa os custos fixos médios.

520 - A curva de custo marginal também é simples:

521 - ...Poderíamos também escrever a definição de custos marginais em termos da função do custo variável (...) Isso equivale à primeira definição, uma vez que c(y) = cv (y) + F, e os custos fixos, F, não variam quando y varia.

522 -  Custos marginais vão empurrar os custos médios para baixo ou para cima. ...Sabemos, portanto, que a curva de custo marginal tem de situar-se abaixo da curva de custo variável médio, à esquerda do seu ponto mínimo e acima dele, à direita. Atenção que o que importa é o "nível abaixo" do custo marginal e não o ponto de inflexão da sua curva, algo que ocorrerá antes dela se cruzar com as demais curvas.

523 - Ainda sobre CVMe: A curva de custo variável médio pode inclinar-se de início para baixo, mas isso não é necessário. Ela, no entanto, poderá crescer, desde que haja fatores fixos restringindo a produção. Muito custo para produzir mais uma "unidade".

524 - ...Vê-se que a curva de custo marginal passa sobre o ponto mínimo tanto da curva de custo variável como da curva de custo médio.

525 - Soma dos custos variáveis:

526 - A partir de uma função de custo, dá pra "tirar" o resto, ao que entendi:

527 - ...A última é a "derivada", claramente. (Cálculo I)

528 - ...Achar o custo médio mínimo? A curva de custo médio alcança seu mínimo quando o custo médio se iguala ao custo marginal.

529 - Quanto se deve produzir em cada fábrica, tendo cada uma delas uma função custo diferente? R = iguala os custos marginais: o custo marginal de produção da fábrica 1 tem de ser o mesmo da fábrica 2. (...) A curva de custo marginal das duas fábricas juntas é apenas a soma horizontal das duas curvas de custo marginal, como mostra a Figura 22.5C.

530 - Produção ótima à minimização de custos (não necessariamente a que maximiza lucro, depende da receita marginal também): a produção total em qualquer custo marginal c será exatamente a soma das produções em que tanto o custo marginal da fábrica 1 como o da fábrica 2 sejam iguais a c: a soma horizontal das curvas de custo marginal.

531 - Sem muita paciência para explicação algébrica/abstrata/chata da lógica das curvas de curto e longo prazo de custos médios. Basta olhar para os gráficos que se entende.

532 - Na prática: ...como só há quatro tamanhos de fábrica diferentes (no exemplo acima), apenas vemos qual deles possui os menores custos associados e o escolhemos. Ou seja, para qualquer nível de produção y, basta escolher o nível de tamanho de fábrica que fornece o custo mínimo de obter esse nível de produção.

533 - Mais interessante me pareceu a ênfase nos "Custos marginais de longo prazo", os quais vão aumentando até caírem bruscamente a cada "pulo" de curva de curto prazo de "nível discreto" (unidade e tal). 

EXERCÍCIOS E APÊNDICE

534 - P = Quais das seguintes afirmações são verdadeiras? (1) Os custos fixos médios nunca aumentam com a produção; (2) os custos médios totais são sempre maiores ou iguais aos custos variáveis médios; (3) o custo médio nunca pode aumentar quando os custos marginais diminuem; R = Verdadeiro; verdadeiro; falso.

535 - Apêndice não acrescenta em relação aos gráficos.

.