Livro: Varian, Hal - Microeconomia (2015) - Parte XV
Livro: Varian, Hal - Microeconomia (2015) - Parte XV
Pgs. 542-570:
CAPÍTULO 20: "Maximização dos lucros"
464 - Premissas/incógnitas - o simples numa linguagem chata: Suponhamos que a empresa produza n produtos (y1 , ..., yn) e utilize m insumos (x1 , ..., xm). Sejam os preços dos bens produzidos (p1 , ..., pn) e os preços dos insumos (w1 , ..., wm). O lucro que a empresa recebe, π, pode ser expresso como
465 - ...Ou... receitas menos custos. Inclusive os custos de oportunidade de não estar vendendo a força de trabalho ou arrendando uma propriedade ou emprestando/aplicando dinheiro.
466 - Como calcular o "custo de oportunidade" ou "taxa de aluguel" das máquinas? Em muitos casos não há um mercado muito bem desenvolvido para o aluguel de máquinas, já que as empresas costumam comprar seus equipamentos. Nesse caso, temos de calcular a taxa de aluguel implícita mediante a verificação de quanto custaria comprar a máquina no início do período e vendê-la no final.
467 - Tamanho e outros fatores são levados em conta para decidir o que uma empresa fará ela própria ou comprará/contratará de terceiros. Uma companhia deve ter o seu próprio restaurante self-service? Serviços de zelador? Serviços de fotocópia? Seus próprios serviços de assistência em viagem?...
468 - Apresenta a ideia de "fatores quase-fixos", diferentes dos fixos (paga mesmo que não produza/use) e dos variáveis (conforme o uso/produção): Eletricidade ...Se a empresa produzir zero, não precisará gastar com iluminação, mas, se produzir qualquer quantidade positiva, terá de comprar uma quantidade fixa de eletricidade para iluminação.
469 - Linguagem algébrica, sei lá pra que, para complicar essa máxima simples aqui: "o valor do produto marginal de um fator deve ser igual a seu preço". Por quê? Se o valor do produto marginal exceder seu custo, os lucros poderão ser aumentados com o aumento do insumo 1. Se o valor do produto marginal for menor do que seus custos, os lucros poderão ser aumentados com a diminuição da quantidade do insumo 1.
470 - ...Ou seja, a maximização do lucro envolve igualar o produto marginal de um fator a seu preço. Em linguagem chata: "o valor do produto marginal, pPM1 (x*1 , x2), deve ser igual ao preço do fator w1".
471 - Mete equação com incógnita que já esqueci o que significa até:
472 - ...Ao menos ele explica um pouco: Essa equação descreve as retas isolucro, que são combinações de insumos e de produtos que fornecem um nível constante de lucros, π. À medida que π varia, obtemos uma família de retas paralelas com uma inclinação w1/p e cada uma delas com um intercepto π/p + w2x2/p , que mede os lucros mais os custos fixos da empresa.
473 - ...Nesse caso, o ponto de maximização do lucro é (x*1zinho , y*1zinho).
474 - ...Vê-se claramente que "o problema da maximização do lucro é, então, achar o ponto da função de produção que esteja associado com a reta isolucro mais alta. Esse ponto é ilustrado na Figura 20.1".
475 - ...a inclinação da função de produção deve igualar a inclinação da reta isolucro.
476 - ...São iguais: ...a inclinação da função de produção é o produto marginal e a inclinação da reta isolucro é w1/p...
477 - Exemplo de "estática comparativa" com a inclinação da reta isolucro em relação à variações de preço. Primeiro do fator x1 (preço w1 aumenta e o "nível ótimo do fator 1 tem de diminuir", usando-se menos dele na produção) e depois simulando a variação de preço do próprio produto. Essa "parte b" do gráfico significa a oferta positivamente inclinada, como já sabido.
478 - Já no longo prazo, todos os insumos são variáveis/substituíveis etc. Vale a:
479 - ...E se a empresa efetuou as escolhas ótimas dos fatores 1 e 2, o valor do produto marginal de cada um dos fatores deve ser igual a seu preço. São x*1 e x*2.
480 - Equação resultantes da escolha ótima são as "curvas de demanda de fatores".
481 - A curva de demanda inversa de fatores mede a mesma relação, mas de um ponto de vista diferente. Ela mede quais devem ser os preços dos fatores para que se demande determinada quantidade de insumos:
482 - Rendimentos constantes de escala e maximização do lucro: em tese, se os insumos são multiplicados por dois, então o lucro também duplicará. Por que não maximizou antes? É que, na verdade o lucro econômico consistente com empresas desse tipo é zero! E zero vezes dois é zero. E se não fosse lucro zero? Em primeiro lugar, a empresa poderia tornar-se tão grande que não conseguiria operar de maneira efetiva. Isso significa apenas dizer que a empresa realmente não tem rendimentos constantes de escala em todos os níveis de produção.
483 - ...Em segundo lugar, a empresa poderia tornar-se tão grande que dominaria totalmente o mercado de seu produto. Nesse caso, não há razão para que ela aja competitivamente – tomando os preços como dados. Ao contrário, faria sentido que a empresa tentasse utilizar seu tamanho para influenciar o preço de mercado. O modelo de maximização do lucro competitivo não seria mais uma forma razoável de comportamento da empresa, já que ela não mais teria concorrentes efetivos. (...) Em terceiro lugar, se uma empresa puder auferir lucros positivos com uma tecnologia de rendimentos constantes de escala, qualquer outra empresa com acesso a essa tecnologia poderá fazer o mesmo. Se uma empresa desejar expandir sua produção, as outras também desejarão o mesmo. Mas, se todas as empresas expandissem sua produção, o preço do produto certamente seria empurrado para baixo, o que diminuiria os lucros de todas as empresas do setor.
484 - Axioma Fraco de Maximização do Lucro (AFML): Se a empresa não respeita a equação abaixo entre dois períodos, então não está agindo como uma maximizadora de lucro:
485 - ....Essa equação é nosso resultado final. Ela diz que a variação no preço do produto multiplicada pela variação na produção menos a variação do preço de cada fator multiplicada pela variação de cada fator não pode ser negativa. Essa equação vem unicamente da definição de maximização do lucro.
486 - ...Por exemplo, vamos supor que examinamos uma situação em que o preço do produto varie, mas o preço de cada fator permaneça constante. Se Δw1 = Δw2 = 0, então a equação (20.7) reduz-se a:
487 - Joga outras fórmulas/vaiorações para tentar complicar conclusões simples. Desconsiderei. Mais atrapalham do que ajudam.
488 - Faz todo uma análise abstrata que sequer sei muito bem o que ele está fazendo na prática. Chama de "estimar tecnologia", seja lá a que problema prático isso se refira. Premissas: "Suponhamos que recebemos uma escolha observada no período t e no período s, que indicamos por (p"t", w"t"1 , y"t", x"t"1) e (p"s", w"s"1 , y"s", x"s"1). Em cada período, podemos calcular os lucros π"s" e π"t" e traçar todas as combinações de y e x1zinho que geram esses lucros". Serão as retas isolucro:
489 - ...Aos preços (p"t", w"t"1), a escolha (y"t", x"t"1) estará na reta isolucro mais alta possível, o que também valerá para a escolha do período s.
490 - ...Isso tudo é para estimar mais precisamente a função de produção. São observadas as escolhas das empresas. "quando as escolhas observadas satisfizerem o AFML, poderemos “reelaborar” uma estimativa de uma tecnologia que poderia haver gerado as observações. Nesse sentido, qualquer escolha observada coerente com o AFML poderia ser uma escolha de maximização do lucro. À medida que observamos mais escolhas feitas pelas empresas, obtemos uma estimativa mais precisa da função de produção, conforme ilustra a Figura 20.5. (...) Essa estimativa da função de produção pode ser utilizada para prever o comportamento da empresa em outros ambientes ou para outros usos em análise econômica". (Obviamente, Varian não perde tempo com exemplos concretos, de como é isso tudo na prática...)
491 - Dá pra ter uma leve ideia do que ele está falando (talvez algo simples):
492 - Sobre subsídios agrícolas - de manutenção do preço artificialmente alto - dos EUA, agricultores argumentam que, se fossem retirados os subsídios, simplesmente aumentariam a produção para manter constante o valor arrecadado e padrão de vida. Não é bem assim que funciona. Como vimos antes, a lógica da maximização do lucro requer que a diminuição do preço de um produto leve à redução da oferta dele: se Δp for negativo, Δy também terá de ser negativo. Não seria lucrativo aumentar a produção sob uma taxa de lucro menor. Já teriam feito isso, se fosse conveniente, à taxa atual (maior). (A tendência, creio, se tentassem, seria o preço baixar mais e mais, até porque não é a mais elástica das demandas...)
EXERCÍCIOS E APÊNDICE
493 - Perguntas e respostas bem mal formuladas, mas fáceis.
494 - Algumas são abertas demais, mas trazem reflexões até razoáveis: P = Maximizar o lucro de uma empresa é sempre o mesmo que maximizar o valor da empresa no mercado de ações?; R = Em geral, não. Pense, por exemplo, no caso da incerteza.
495 - A oito eu nem entendi. Deve estar se referindo a lucros econômicos e não ao lucro contábil.
496 - Pra variar, não vi a utilidade do apêndice. Sei nem que problema está resolvendo, se estiver.
.
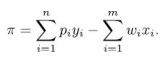







Comentários
Postar um comentário