Livro: Varian, Hal - Microeconomia (2015) - Parte III

           

Livro: Varian, Hal - Microeconomia (2015) - Parte III

Pgs. 114-140:

CAPÍTULO 4: "Utilidade"

68 - Num momento "meio HPE", afirma que a ideia de utilidade era muito vaga. Esses problemas conceituais levaram os economistas a abandonar a velha visão da utilidade como medida de felicidade e a reformular toda a teoria do comportamento do consumidor com base nas preferências do consumidor. A utilidade passou a ser vista somente como um modo de descrever as preferências.

69 - A função de utilidade é um modo de atribuir um número a cada possível cesta de consumo, de modo que se atribuam às cestas mais preferidas números maiores que os atribuídos às menos preferidas. (...) u(x1 , x2) > u(y1 , y2).

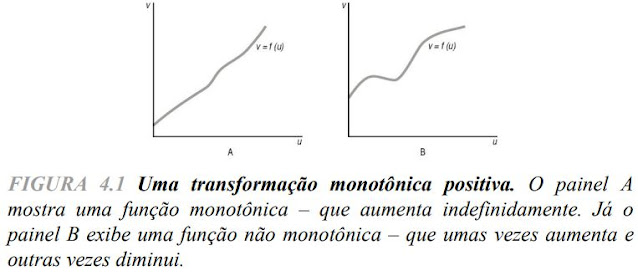
70 - É mais um capítulo onde o autor parece iniciar mais preocupado em apresentar conceitos do que, ironicamente, explicar a utilidade prática deles. Ou mesmo partir dela, dos problemas que resolve e tal. Enfim, cabe a mim transcrever um ou outro: A transformação monotônica é em geral representada pela função f(u), que transforma cada número u em outro número f(u), mas preserva a ordem dos números para que u1 > u2 implique f(u1) > f(u2). Exemplo de transformação desse tipo: "elevação de u a alguma potência ímpar (por exemplo, f(u) = u elevado à terça)"

71 - ...Como todas as cestas de uma curva de indiferença precisam ter a mesma utilidade, a função de utilidade constitui um meio de atribuir números às diferentes curvas de indiferença, para que as mais altas recebam números maiores.

72 - Nem todos os tipos de preferências podem ser representados pela função de utilidade. Suponhamos, por exemplo, que alguém tenha preferências intransitivas, de modo que A > B > C > A. Essa preferência não teria lógica numa função utilidade. A solução é óbvia: ...se excluirmos casos perversos como as preferências intransitivas, em geral conseguiremos encontrar uma função de utilidade para representar as preferências.

73 - Continuo sem entender a utilidade da função de utilidade, mas estou acompanhando com atenção:

74 - E se o consumidor quisesse substituir o bem 1 pelo bem 2, por uma taxa diferente de 1 por 1? Suponhamos, por exemplo, que o consumidor exija duas unidades do bem 2 para compensá-lo pela desistência de uma unidade do bem 1. Isso significa que, para o consumidor, o bem 1 é duas vezes mais valioso do que o bem 2. A função de utilidade assume, portanto, a forma u(x1 , x2) = 2x1 + x2 . Observemos que essa utilidade produz curvas de indiferença com uma inclinação de –2.

75 - Apresenta, também sem qualquer menção à realidade prática, o conceito de "preferência/utilidade quase linear": 

76 - Função utilidade Cobb-Douglas: x1 e x2 elevados a "c" e "d" respectivamente, sendo que c e d são números positivos que descrevem as preferências do consumidor.

77 - ...As preferências Cobb-Douglas são o exemplo típico de curvas de indiferença bem-comportadas, e, de fato, a fórmula que as descreve é a expressão algébrica mais simples que gera preferências bem-comportadas.

78 - A partir disso, Varian faz observações abstratas. Vou transcrever a mais simples dela (ele faz outra e diz que é importante, mas não explica a importância, não me interessei): As curvas de indiferença dessa função de utilidade terão a mesma forma que as curvas de indiferença da primeira função Cobb-Douglas, uma vez que o logaritmo é uma transformação monotônica.

79 - Sempre do abstrato para (talvez/às vezes) o concreto, joga a fórmula da utilidade marginal:

Mesma fórmula, arrumação diferente...

80 - Imaginemos uma variação no consumo de cada bem (Δx1 , Δx2), que mantenha a utilidade constante – isto é, uma variação no consumo que nos mova ao longo da curva de indiferença. Devemos ter, então, UM1Δx1 + UM2Δx2 = ΔU = 0. Rearruma para buscar a inclinação:

81 - Faz uma observação: ...pode ser tedioso acompanhar sempre esse irritante sinal de menos, de modo que os economistas costumam referir-se à TMS pelo valor absoluto dela – isto é, por um número positivo. Seguiremos essa convenção sempre que isso não causar confusão

82 - Joga regras e "exemplos" no abstrato: ...Assim, se, por exemplo, multiplicarmos a utilidade por 2, a utilidade marginal será também multiplicada por 2... A razão das utilidades marginais independe da transformação específica da função de utilidade que se queira utilizar... Embora as utilidades marginais sejam alteradas pelas transformações monotônicas, a razão das utilidades marginais independe da forma específica escolhida para representar as preferências. Exemplo:

83 - Partindo pro concreto, propõe um modelo que medisse as preferências do consumidor por carro (custos e tempos representados por x) ou por ônibus (custos e tempos representados por y).

84 - ...Obs.: Qualquer transformação monotônica dessa função de utilidade descreveria igualmente bem o comportamento de escolha, mas a forma linear é bem mais fácil de usar do ponto de vista estatístico. 

85 - ...Pois bem, como foi feito e pra que serviu? Vamos supor agora que observamos diversos consumidores semelhantes a escolher entre o carro e o ônibus, com base no padrão específico de tempo de transporte, custos etc. com que se defrontam... (parece uma coleta de dados bem difícil/chata, por sinal)

86 - ...A razão entre um coeficiente e outro avalia a taxa marginal de substituição entre uma característica e outra. Por exemplo, a razão entre a utilidade marginal do tempo percorrido a pé e a utilidade marginal do tempo total indica que o consumidor típico considera o tempo percorrido a pé cerca de três vezes mais oneroso do que o tempo de viagem.

87 - ...Nesse estudo, o usuário típico atribuiu a cada minuto de tempo de viagem um valor de 0,0411/2,24 = 0,0183 dólar, o que equivale a US$1,10 por hora. Para fins comparativos, o salário por hora do usuário típico em 1967, o ano do estudo, era de, aproximadamente, US$2,85.

88 - ...Essas estimativas de funções de utilidade podem ser muito valiosas para determinar se vale ou não a pena promover alterações no sistema de transporte público. Por exemplo, na função de utilidade que acabamos de descrever, um dos fatores significativos para explicar a escolha do meio de transporte era o tempo gasto para fazer a viagem. As autoridades de transportes poderiam, a um custo adicional, colocar mais ônibus em circulação para reduzir o tempo de deslocamento. Será, porém, que o número de novos passageiros compensaria o aumento das despesas? (...) A partir de uma função de utilidade e de uma amostra de consumidores, é possível prever quais consumidores usarão o carro e quais escolherão o ônibus. Isso dará uma ideia de se a receita será suficiente para cobrir o custo adicional.

89 - ...Além disso... Já vimos no estudo de Domenich e McFadden que, em 1967, o usuário típico atribuía ao tempo de transporte um valor de aproximadamente US$1,10 por hora. Ele estaria, pois, propenso a pagar aproximadamente US$0,37 para reduzir em 20 minutos o tempo de viagem. Esse número nos dá uma medida do benefício, em dólares, de aumentar a frequência de circulação dos ônibus. Esse benefício tem de ser comparado ao custo de ampliação dos serviços para saber se vale a pena fazer isso.

90 - (Enfim, estudo interessante, mas não me imagino fazendo ou me interessando realmente. Microeconomia, até agora, no meu contexto, acaba sendo meio que uma boa curiosidade apenas. Os dois meses que dedicarei à mesma me parecem até muito. Estudo por achar que pode ter alguma repercussão na macro)

EXERCÍCIOS E APÊNDICE

91 - P = Que tipos de preferências são representados pela função de utilidade com u(x1 , x2 )-raiz quadrada de x1zinho + x2zinho? E pela função de utilidade v(x1 , x2 ) = 13x1zinho + 13x2zinho? R = Ambos representam substitutos perfeitos.

92 - Questão seis: 

93 - P = Você pode explicar por que a transformação monotônica de uma função de utilidade não altera a taxa marginal de substituição? R = Porque a TMS é medida ao longo de uma curva de indiferença, ao longo da qual a utilidade permanece constante.

94 - O apêndice - de três páginas - é bem interessante pra quem tiver mais curiosidade sobre a matemática do capítulo. Dei uma passada por cima. Não me demorei por não ver utilidade prática para mim, mas deu pra lembrar de algumas coisas.

.